六方最密構造(hcp hexagonal closedpacked) 体心立方格子(bcc body centered cubic) ダイヤモンド構造 最密充填構造 配位数=12 最密充填構造 配位数=12 配位数=8 配位数=4 sp3 混成軌道の4ボンドの制約下で最密充填 最近接原子距離 = 第2最近接原子距離 = a構造 鎖状構造 平面層構造 安定条件 Mardelung 定数 1386 !デバイスに用い(られてい)る半導体 Si, Ge, ダイアモンド構造 GaAs, InP, InAs, InSb, 閃亜鉛鉱構造 GaN ウルツ鉱構造
2
ダイヤモンド構造 充填率 計算
ダイヤモンド構造 充填率 計算- 覚え方・暗記法に悩む 高校生・既卒生・大学受験生向けの、 高校化学に関する語呂合わせブログです。 化学反応式や構造、 考え方や計算の手順、 大学入試化学の過去問などを、 語呂合わせやちょっとしたコツ、 分かりやすいフレーズで 解説します。 16一部・17・18・18追試結晶構造の例 各種構造の充填率の導出 理想結晶による干渉性散乱強度 逆ベクトル,逆格子および面間隔 単位胞の体積 結晶構造因子の計算:一種原子の簡単な例 ダイヤモンド構造の 各面の原子配列をそれぞれ描け.



結晶
したがって、ダイヤモンドの単位格子における配位数は 4 となる。 黒鉛 黒鉛cは、炭素原子がもつ4コの価電子のうち3コのみを使って隣り合う炭素原子の価電子と共有結合し、正六角形の構造が繰り返された 平面層状構造 を作っている。また、この平面ダイヤモンド型構造 ダイヤモンドでは,結合を4つ持ったテトラポッド型の炭素原子どうしが 共有結合で結合し,立体的な網目構造を作っている.炭素原子はsp3混 成状態を取っている.その他に,Si,Geもダイヤモンド型構造を取る. 受験対策サイトへようこそv (*^ ^*)v /5/13 数Ⅱ:式と証明の全面改訂を完了し、pdfの販売を開始。 /6/22 数Ⅱ:複素数と方程式の全面改訂を完了し、pdfの販売を開始。 /8/19 数Ⅱ:三角関数の全面改訂を完了し、pdfの販売を開始。 数B
金属結晶構造では、学習内容と受験で出題される範 囲から、以下の3 点を学ぶことができ、低コストで 生徒にも自作できる教材を製作した。 (a)単位格子中の原子数 (b)配位数:ひとつの原子に配位する原子の数 (c)空間充填率:単位格子中に原子が占める割合(f) ダイヤモンド型 ダイヤモンド C C 8個 — (g) 六方最密格子(hcp)マグネシウム Mg Mg 2個 — (f) — グラファイト C C 4個 — 3種類の立方格子の充填率を計算によって確かめよ。 (a) 面心立方格子(立方最密充填)74% (b) 体心立方格子 68%充填率 単位体積あたりの原子の体積 占有率 格子定数(lattice constant) 格子の単位となる長さ(図36のa) 図35単位格子の例 金属の結晶構造 (1) 体心立方格子(BCC) (2) 面心立方格子(FCC) (3) 六方最密格子(HCP) 322体心立方格子(body centered cubic lattice, BCC)
332 温度とヤング率の関係 図39に示すようにポリマーのヤン グ率は温度に強く依存する. (1)ガラスプラトー(T≪Tg) ポリマー分子の共有結合と2次結 合がヤング率を支配する領域 共有結合率f 共有結合(ヤング率E1)が占める 割合.残り(1f)の領域は2次結球を平面に敷き詰めると,最密充填構造は図1(a)のようになり,球 ①の周りには球②~⑦が接する。次に,この第1層上に球を最密に 敷き詰めるため,図1(b)のように,第1層にできたくぼみの上に球⑧ ~⑩の要領で球を積み重ね,これを第2層とする。イオン半径から r A/r B を計算し、安定条件を満たす最も 配位数の大きな構造をとる イオン結合 ZnS 構造 NaCl 構造 CsCl 構造
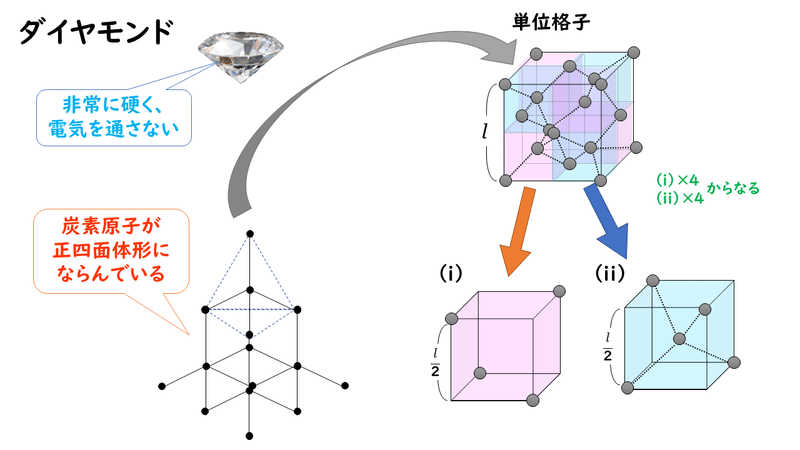



見落とす モットー テロ ダイヤモンド 充填率 求め方 Godengine Jp



2
問2 充填率 単原子分子(球形)fccおよびダイヤモンドの充填率を求め、その違いを結合の視点から説明せよ。 問3 充填率 Na金属(bcc, 格子間隔366 Å)で、Naのイオン半径を116 Åとすれば、Naのイオン殻の充填率を求めよ。 問4 水素 6 結晶の表現方法 (1)方向 基本格子ベクトルをa, b, c とし,n1, n2, n3 を任意の公約数を持たない整数とすると,ベクトル T = n1 a n2 b n3 c (11) の整数倍によって1つの単位胞を任意の単位胞の位置に移動させて重ね合わせることができる.n1, n2, n3 を複合材料の熱伝導率は計算によってシミュレーションする ことができる。複合材料の熱伝導率の計算式としてMaxwell の式が古くから知られている 38)。次式はMaxwell の式で金 属/ダイヤモンド複合材料の熱伝導率を表記したものである。 k k d kV d m k d k m k d m



2




17 号 反射防止膜 光学部材及び光学部材の製造方法 Astamuse
空間が原子の球によって占められる割合を充填率といいます。 (1) 面心立方構造(最密充填) ダイアモンド構造 の充填率を計算してください。 0740 2 2 3 4 1 3 3 3 u r Sr (2) 体心立方構造 (3) ダ六方最密充填構造においても、同様に充填率を算出することができる。六角柱の一辺をa 、高さをc とおくと、 =, = となり、これを用いて充填率APFを計算すると、 = = (/) () / = となる。 各種の構造における充填率 同様の方法を使えば、どの結晶構造についても空間充填率の理論値を求める面の中心に原子が位置する面心立方格子が原子の充填率が一番大きい。特に(111) 面と呼ぶ面が充填率が大 きい。半導体材料として良く知られたSi やGeは、面心立方格子とは基本的に同じダイヤモンド構



結晶化学



2
構造 鎖状構造 平面層構造 安定条件 Mardelung 定数 1386 1542 1638 1748 1763 3 1 rr AB t 21rr AB t 31 AB 2 rrt # 0225 # 0414 # 0732 23 1 AB 3 rrt # 0155 配位数の大きなものがより安定 (Mardelung 数が大) イオン半径から r A /r B を計算し、安定条件を満たす最も配 位数の大きなこれより、ダイヤモンド c の充填率は、約 34% と隙間の多い構造であることが分かります。 また、ダイヤモンド C の密度は、アボガドロ定数を N A 、体積を a 3 cm 3 、原子量を 12 とすると、次のよダイヤモンド構造 充填率 ダイヤモンド構造 充填率高3 化学 物質の状態 高校生 化学のノート Clear 高校化学 結合 金属結晶 結晶格子 オンライン無料塾 ターンナップ Youtube 結晶 ダイヤモンド型結晶格子の計算問題 Youtube



2




15 号 銅 ダイヤモンド複合材及びその製造方法 Astamuse
体心立方格子(配位数・充填率・密度・格子定数・半径など) プロ講師解説金属の単位格子は 面心立方格子 ・体心立方格子・ 六方最密構造 に分類することができます。 このページではそのうちの1つ、体心立方格子について、配位数や充填率、密度 覚え方・暗記法に悩む 高校生・既卒生・大学受験生向けの、 高校化学に関する語呂合わせブログです。 化学反応式や構造、 考え方や計算の手順、 大学入試化学の過去問などを、 語呂合わせやちょっとしたコツ、 分かりやすいフレーズで 解説します。 16一部・17・18・18追試スライドの訂正 体心立方格子の充填率の計算 4→2 2 3 7月18日 (1)格子定数a の体心立方格子を考える. (11) 単位格子を図示せよ. (12) (110)面および 方向を図示せよ. (2)結晶内にある一組の面のひとつが軸と3a,2b,2cで交わる.こ



2



2
創立25 周年記念特集「計算熱物性25 年の歩み」 185 特集 単層カーボンナノチューブの熱伝導 Heat Conduction of SingleWalled Carbon Nanotubes 丸山茂夫* Shigeo Maruyama ナノテク新素材として知られる単層カーボンナノチューブの熱伝導率は,ダイヤモンドを超えるとここで,セロハンテープの複屈折率を考える.屈折率と は,媒質中を進む光波の進行速度が遅くなる割合のことで ある.「水の屈折率は133」等ということがあるが,これは 言い換えれば「水中を進む光の速度は,真空中に比べ133化学授業実践記録 イメージ作りを重視した化学 II の授業実践 新潟県立新潟高等学校 大平和之 はじめに 「化学 II 理論分野の内容は公式を覚えただけでは難関校の問題は解けない。 演習問題を繰り返し解くことで『問題上でどんなことが起こっている



高校化学 結晶格子i 金属結晶 体心立方格子 理論化学 Okedou



特許 知財ポータル Ip Force
ダイヤモンド型構造において、交互に 空間が原子の球によって占められる割合を充填率といいます。 (1) 面心立方構造(最密充填) (2) 体心立方構造 (3) ダイアモンド構造 の充填率を計算してください。




暗記不要 ダイヤモンドの密度の求め方をまとめてみた 化学受験テクニック塾



2




空間充填率 Wikiwand



2



金属の結晶格子を仕組みから徹底解説 受験メモ




単純立方格子状に自己集合するコロイド半導体量子ドット 理化学研究所




固体の構造と状態変化 単位格子から原子量を求める方法がわかりません 化学 定期テスト対策サイト
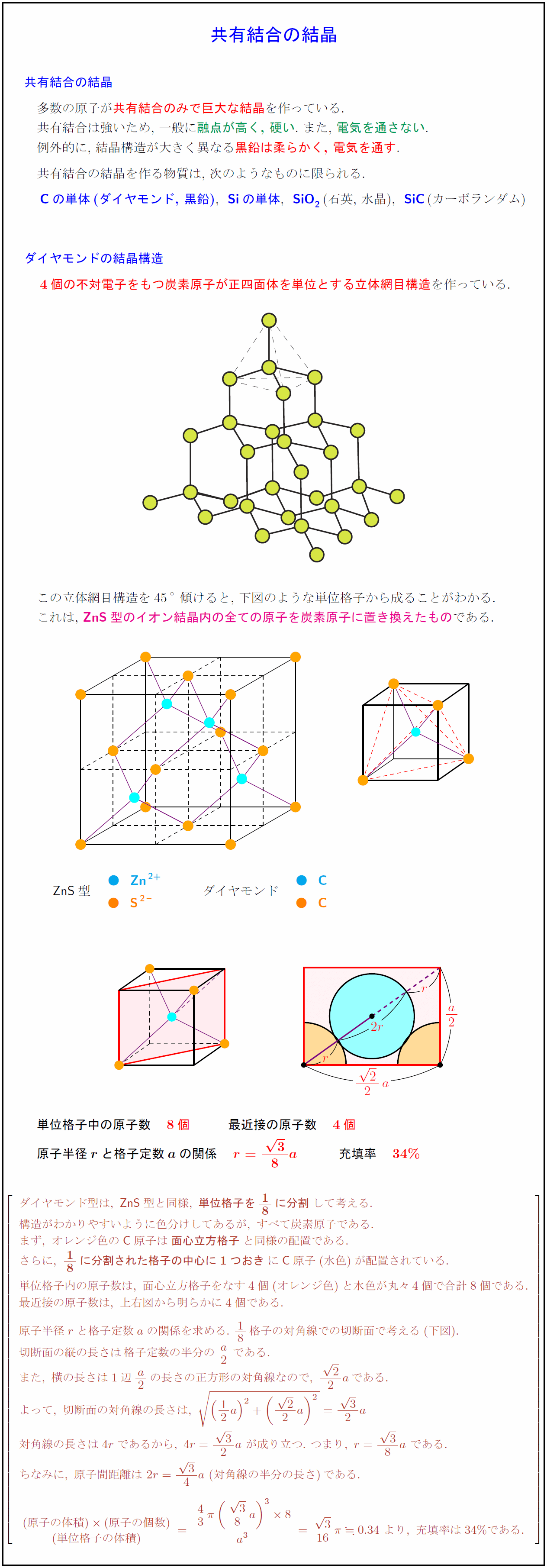



高校理論化学 共有結合の結晶 ダイヤモンドの結晶構造 受験の月




発展問題 氷の構造など Shinshu Univ Physical Chemistry Lab Adsorption Group



2




金属結晶 充填率 格子一辺の長さ 原子半径 高校化学 エンジョイケミストリー Youtube




金属結合と金属結晶
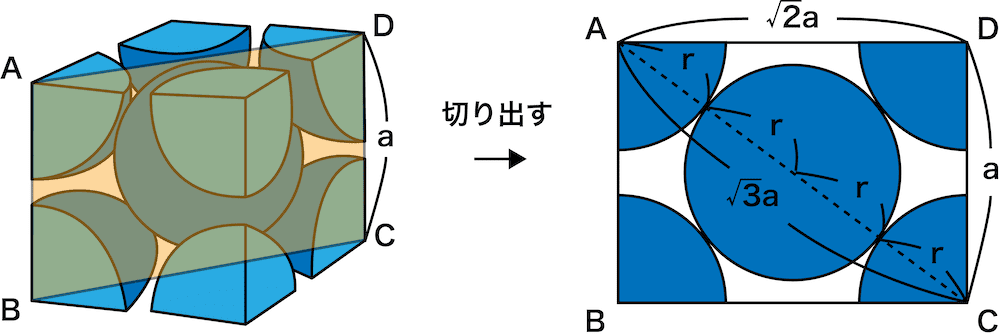



体心立方格子 配位数 充填率 密度 格子定数 半径など 化学のグルメ
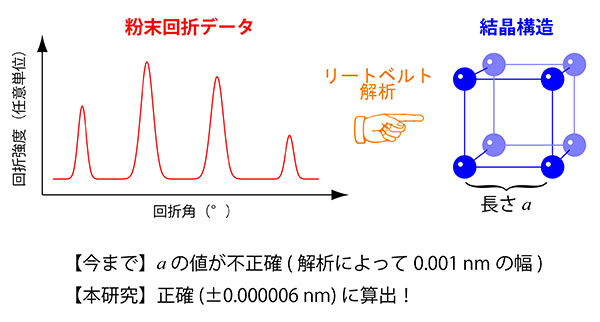



粉末材料の結晶構造を正確に解析可能に リートベルト法でより正確な格子パラメーターを得るには Academist Journal



1



2



2



2



結晶化学



金属の結晶格子を仕組みから徹底解説 受験メモ



2



結晶化学
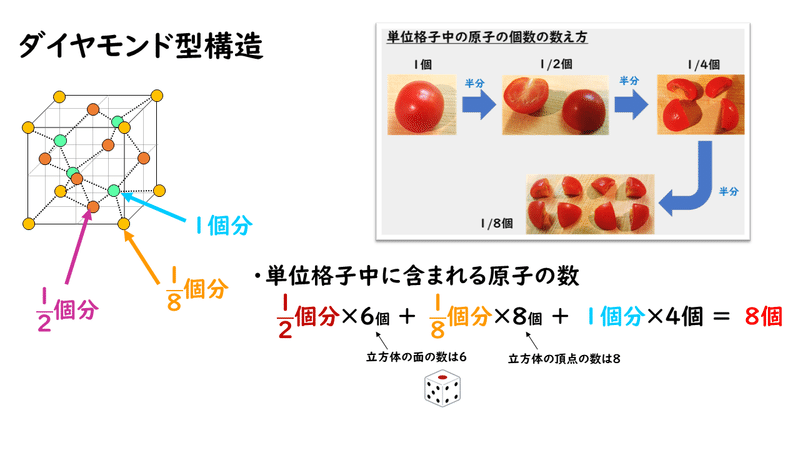



見落とす モットー テロ ダイヤモンド 充填率 求め方 Godengine Jp



2
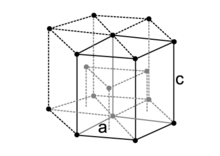



空間充填率 Wikipedia




覚えて安心 ダイヤモンドの充填率の覚え方 語呂合わせ 体心立方格子 面心立方格子 六方最密構造の充填率の覚え方 語呂合わせ ダイヤモンドの構造の見方 単位格子 ゴロ化学 Youtube
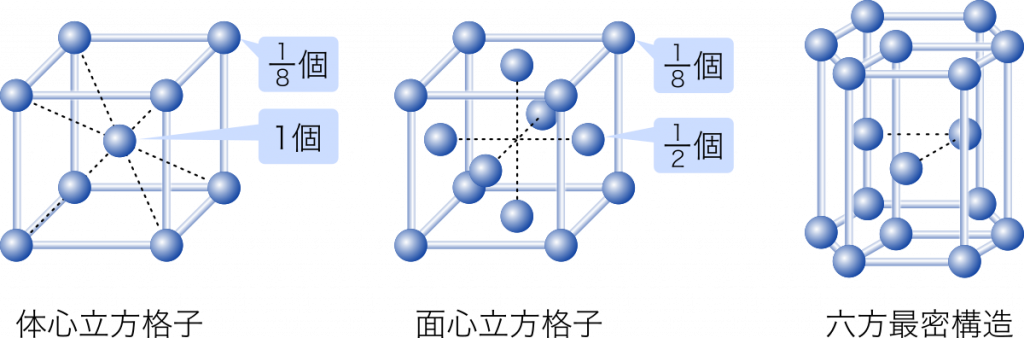



高校化学基礎まとめ 金属結晶の充填率の求め方 Mm参考書
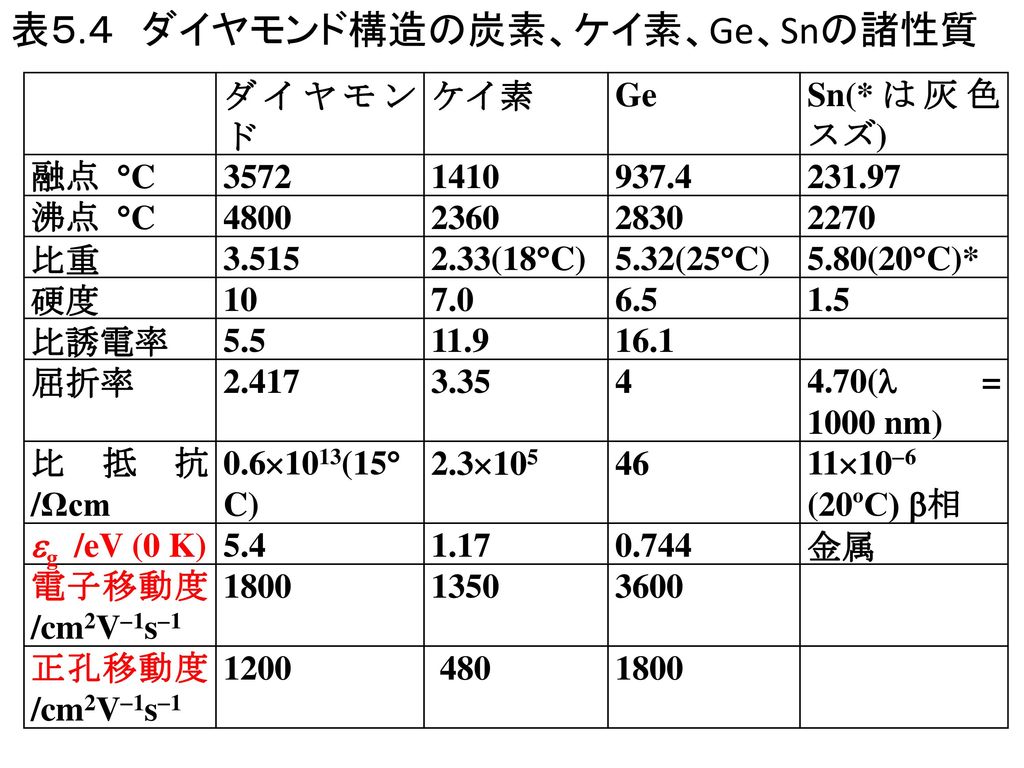



5 4 1 14族 C Si Ge Sn Pb C Siが非金属元素に分類されるが Ge Asnは半導体 金属でない Ppt Download




高校化学基礎まとめ 金属結晶の充填率の求め方 Mm参考書



2



見落とす モットー テロ ダイヤモンド 充填率 求め方 Godengine Jp




19センター化学 第1問 問2 単位格子 充填率の語呂合わせ 語呂合わせで高校化学 大学入試ゴロ化学




専門 講義 結晶構造について 大学生 専門学校生 社会人 工学のノート Clearnote



3



2



高校理論化学ダイヤモンドの充填率について 写真のように一辺の長さをaと Yahoo 知恵袋



2
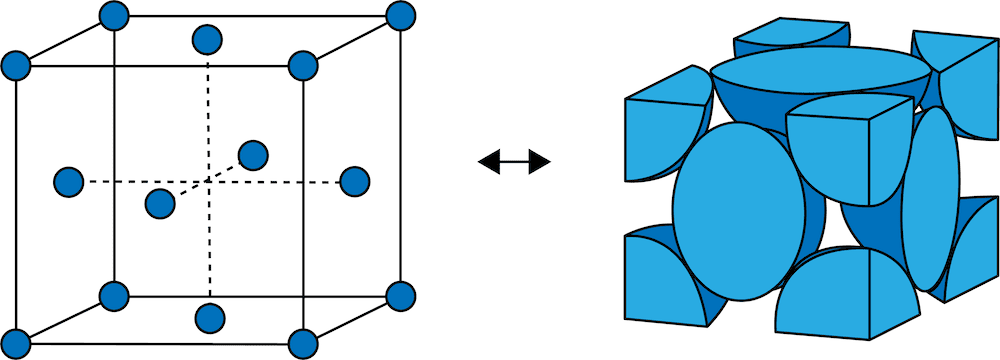



上 ダイヤモンド構造 充填率 計算 2260 ダイヤモンド構造 充填率 計算 Mbaheblogjpzmem




ダイヤモンド型構造 坂根弦太のdv Xa Venus日誌




12ページ目の 授業 高校化学の教材 分子と結晶模型の ベンゼン屋 楽天ブログ




ねがてぃぶろぐ Akaikkrでダイヤモンド型構造半導体



結晶



上 ダイヤモンド構造 充填率 計算 2260 ダイヤモンド構造 充填率 計算 Mbaheblogjpzmem




上 ダイヤモンド構造 充填率 計算 2260 ダイヤモンド構造 充填率 計算



Cc Miyazaki U Ac Jp
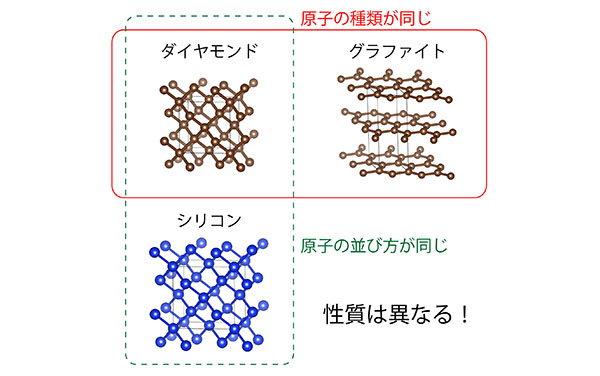



粉末材料の結晶構造を正確に解析可能に リートベルト法でより正確な格子パラメーターを得るには Academist Journal



2




19センター化学 第1問 問2 単位格子 充填率の語呂合わせ 語呂合わせで高校化学 大学入試ゴロ化学



2



2



File Chemnote Hyakunin Isshu Net



ダイヤモンドの充填率の求め方を教えてください 一辺は3 56 10 8cm Yahoo 知恵袋
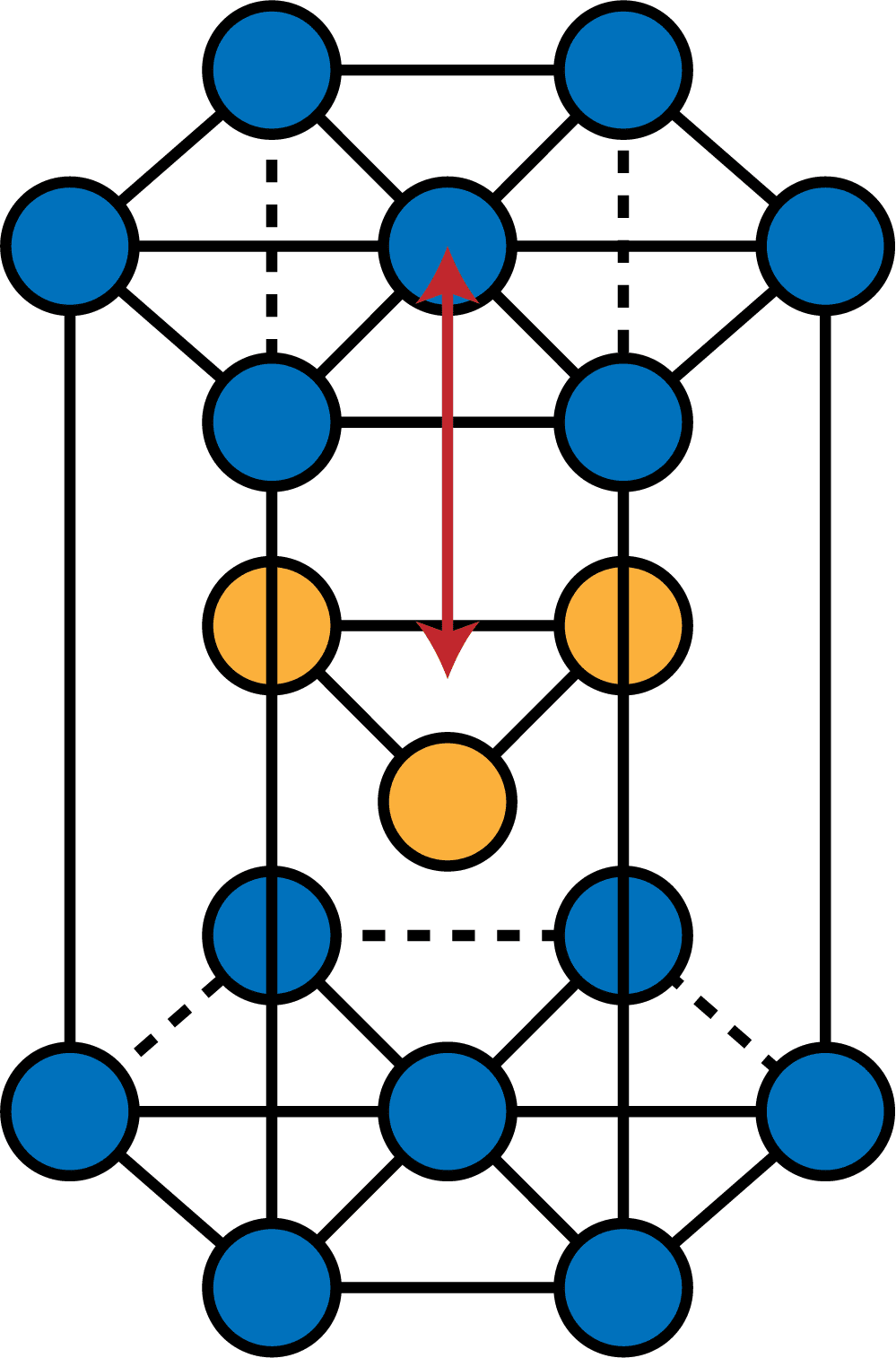



六方最密構造 単位格子に含む原子数 配位数 高さ 充填率の求め方など 化学のグルメ
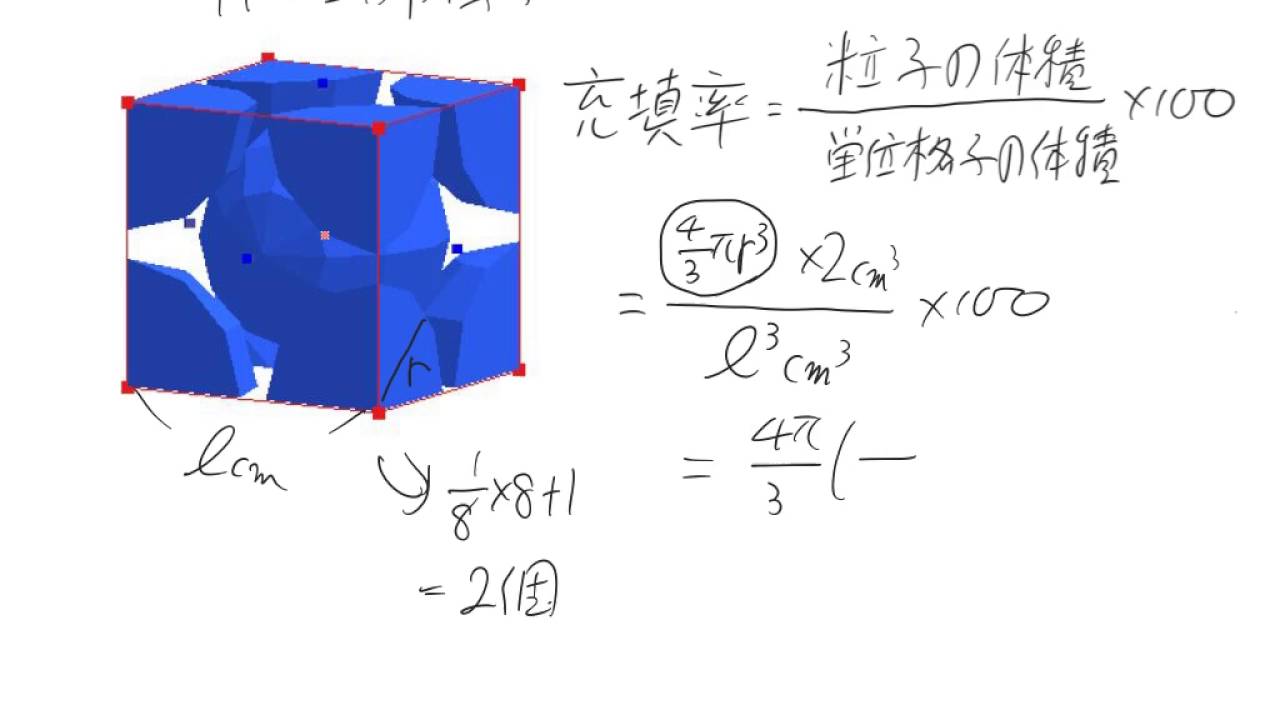



体心立方格子の充填率 Youtube



金属の結晶格子を仕組みから徹底解説 受験メモ



Cgl通信 中央宝石研究所 Cgl




暗記不要 ダイヤモンドの密度の求め方をまとめてみた 化学受験テクニック塾



1




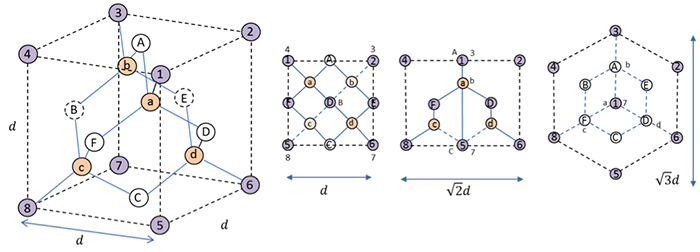
ダイヤモンド構造 111面 通常ダイヤモンドは 六角形を交互ずらすように 111 方向に積層した構造である 図7
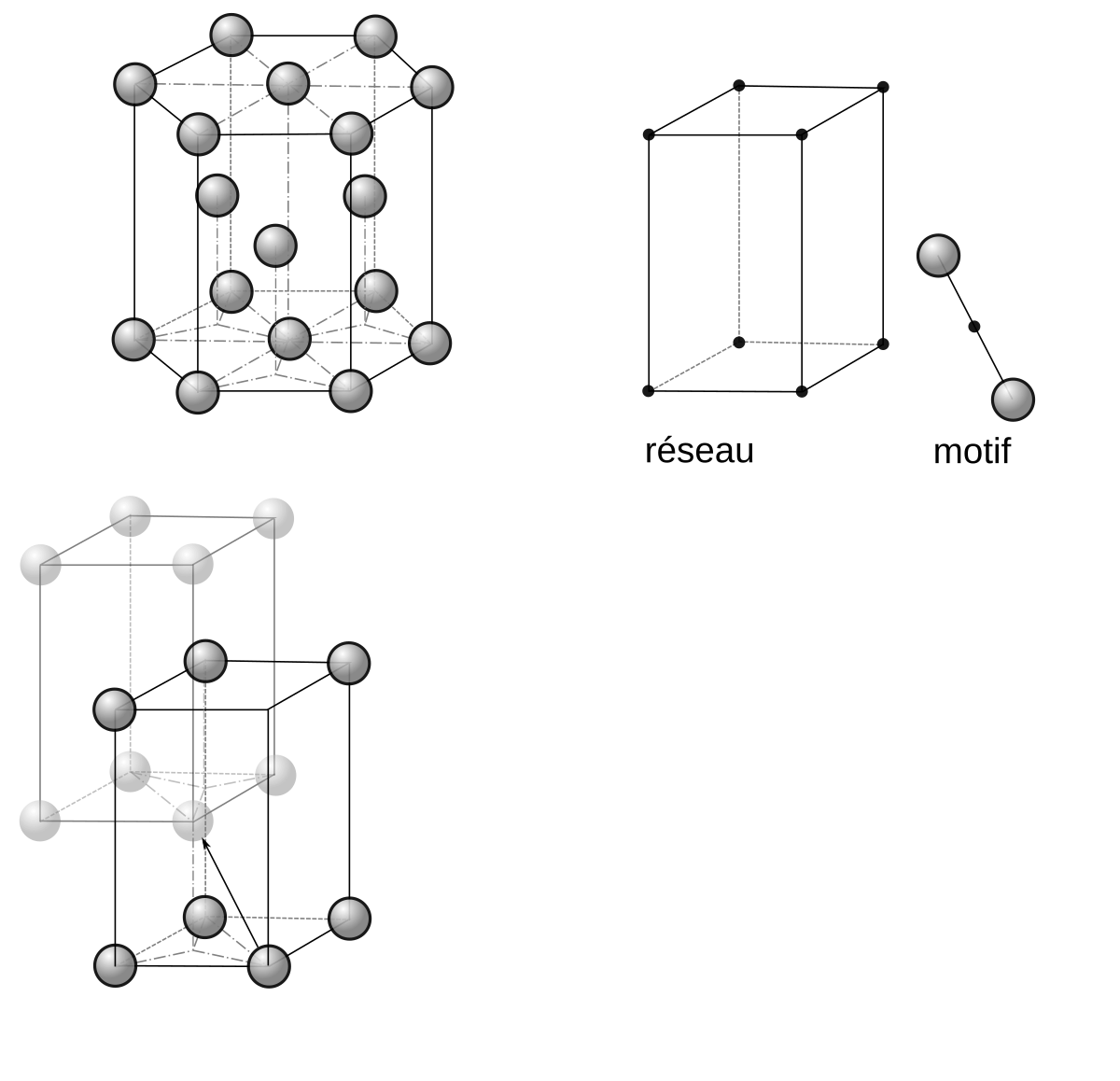



六方最密充填構造 Wikipedia



2




暗記不要 ダイヤモンドの密度の求め方をまとめてみた 化学受験テクニック塾




フレッド ブレスレット用バックル ダイヤ ダイヤモンド フォース10 Mm ハーフ K18pg セラミック 中古 Blj Fitzfishponds Com




発展問題 氷の構造など Shinshu Univ Physical Chemistry Lab Adsorption Group




単分散ナノダイヤモンドとその応用




h29センター化学第1問 問2 単位格子に含まれる原子数 配位数 充填率の語呂合わせ 語呂合わせで高校化学 大学入試ゴロ化学



結晶
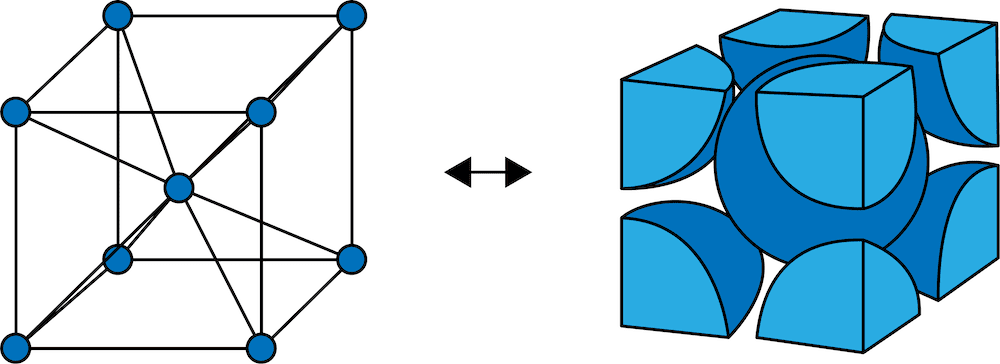



体心立方格子 配位数 充填率 密度 格子定数 半径など 化学のグルメ



Information




高校化学 充填率 映像授業のtry It トライイット
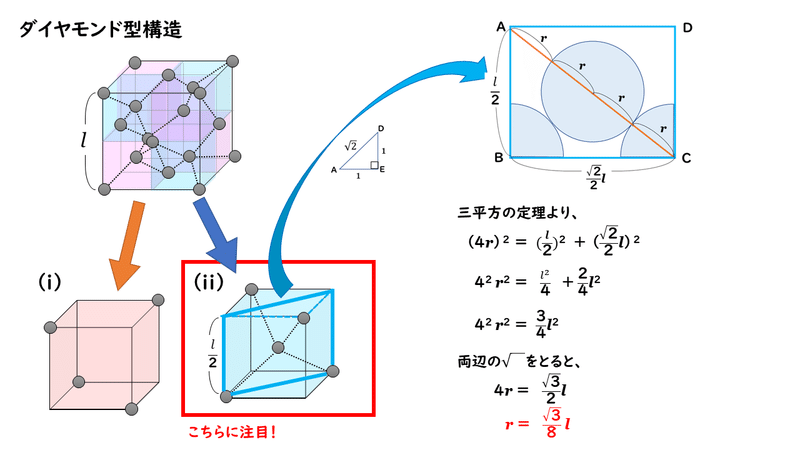



サイクル メーカー 雄弁 ダイヤモンド 密度 求め 方 Tanukiadventure Org




ダイヤモンド型構造 坂根弦太のdv Xa Venus日誌



第3節 物質の構成粒子




買い物 オーロラ調グラデーションが美しい西川の毛布敷きパッド 西川 毛布 敷きパッド シングル オーロラ調 毛布敷きパッド グラデーション 東京西川 毛布パッド 毛布敷き パッドシーツ




19センター化学 第1問 問2 単位格子 充填率の語呂合わせ 語呂合わせで高校化学 大学入試ゴロ化学




無機化合物の構造と特性 との関係を理解する Ppt Download



2




ダイヤモンド型結晶の問題解法 覚えるべき事4選 化学受験テクニック塾



コラム 屈折率 構造システム グループ




目で見て操作する 分子の世界 そのミクロ構造と物性 物質の構造




空間充填率 Wikipedia



危険物甲種についてです 次の図は 金属結晶の単位格子の一 Yahoo 知恵袋
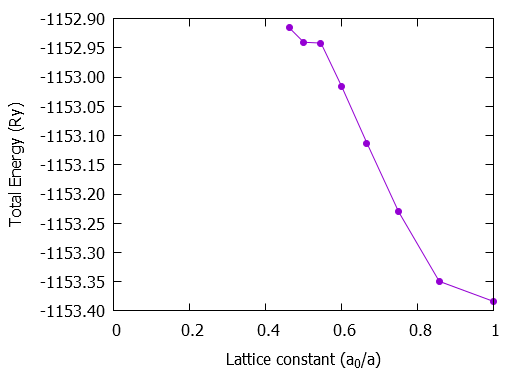



ねがてぃぶろぐ Akaikkrで凝集エネルギー 未完



2




結晶格子に関する問題 完全攻略チャート 過去問解説集 自宅でできる受験対策ショップ ワカルー Wakaru



ダイヤモンドの充填率の出し方がわかりません 答えは34 となるようで Yahoo 知恵袋




単分散ナノダイヤモンドとその応用



1



2



2



2



2


